Function and Limit of a Complex Variable

Functions and Mappings

Anggap $S$ adalah himpunan bilangan kompleks. Sebuah fungsi $f$ yang didefinisikan terhadap $S$ adalah aturan yang menghubungkan setiap bilangan kompleks $z$ dalam $S$ dengan tepat satu bilangan kompleks $w$ . Sehingga $w = f(z)$ dimana $S$ adalah domain dari $f$ dan $w$ adalah nilai dari $f$ pada $z$ .

Contoh:

Jika $f$ didefinisikan untuk set $z \neq 0$ sebagai $w = 1/z$ , anggap $u + iv$ adalah nilai dari fungsi $f$ pada $z = x + iy$ . Maka

u + iv = f(x + iy)

Setiap nilai real $u$ dan $v$ memiliki hubungan terhadap real $x$ dan $y$ , sehingga $f(z)$ bisa diekspresikan dalam bentuk pasangan bilangan real $x$ dan $y$ :

\begin{equation} f(z) = u(x, y) + iv(x, y) \end{equation}

Contoh:

Jika $f(z) = z^2$ , maka

f(x + iy) = (x + iy)^2 = x^2 - y^2 + 2ixy

sehingga

u(x, y) = x^2 - y^2 \quad \text{dan} \quad v(x, y) = 2xy

Jika nilai $v$ dalam persamaan (1) adalah nol, maka fungsi $f$ disebut sebagai fungsi real. Sehingga $f$ adalah real-valued function dari sebuah bilangan kompleks.

Contoh:

Sebuah fungsi real yang penting adalah

f(z) = |z|^2 = x^2 + y^2 + i0

Jika $n$ adalah bilangan bulat positif dan $a_0, a_1, \ldots, a_n$ adalah konstanta kompleks, dimana $a \neq 0$ ,

P(z) = a_0 + a_1z + a_2z^2 + \ldots + a_nz^n

adalah fungsi polinomial berderajat $n$ .

Bentuk rasio $P(z)/Q(z)$ dimana $P(z)$ dan $Q(z)$ adalah polinomial, disebut sebagai fungsi rasional dan terdefinisi untuk setiap $z$ dimana $Q(z) \neq 0$ .

Jika menggunakan koordinat polar $r$ dan $\theta$ , maka

u + iv = f(re^{i\theta})

dimana $w = u + iv$ dan $z = re^{i\theta}$ dapat dituliskan

\begin{equation} f(z) = u(r, \theta) + iv(r, \theta) \end{equation}

Contoh

Terdapat sebuah fungsi $w = z^2$ ketika $z = re^{i\theta}$

\begin{align*} w &= (re^{i\theta})^2 = r^2e^{i2\theta}\\ &= \underbrace{r^2\cos(2\theta)}_{u(r, \theta)} + i\underbrace{r^2\sin(2\theta)}_{v(r, \theta)} \end{align*}

Konsep multiple-valued function terjadi dalam variabel kompleks sebagaimana dalam fungsi real. Jika hal ini terjadi, biasanya hanya satu nilai dari fungsi yang dipilih sebagai nilai utama.

Contoh:

Kita tahu bahwa $z^{1/2}$ memiliki 2 nilai:

z^{1/2} = \pm \sqrt{r}\exp\left(\frac{i\theta}{2}\right)

dimana $r = |z|$ dan $\pi < \theta \leq \pi$ adalah argumen dari $z$ . Jika kita hanya memilih nilai positif dari $\pm \sqrt{r}$ , maka

f(z) = \sqrt{r}\exp\left(\frac{i\theta}{2}\right) \quad (r>0, \ \pi < \theta \leq \pi)

$\text{Multivalued Function}$

Fungsi ini tidak dipandang sebagai fungsi yang normal, i.e. one-to-one atau many-to-one. Jika fungsi trigonometri, hiperbolik, eksponensial, dan perpangkatan bilangan bulat adalah single-valued function, maka fungsi inversnya adalah multi-valued function.

Sebagai contoh $\sqrt{z}$ mapping ke 2 nilai berbeda yaitu $\pm \sqrt{r}\exp\left(\frac{i\theta}{2}\right)$ . Meskipun nilai principal value dapat dipilih dari kasus ini (nilai positifnya saja), namun tidak bisa kontinu di seluruh bidang kompleks sehingga terjadi diskontinuitas.

Complex Functions as Mappings

Kita dapat menginterpretasikan poin-poin $z = (x, y)$ dan $w = (u, v)$ dalam dua bidang yang berbeda karena $z \mapsto w$ membutuhkan visualisasi 4 dimensi.

Contoh:

w = z + 1 = (x + 1) + iy

mentranslasikan setiap poin $z$ sebesar 1 ke kanan. Berikutnya, untuk $i = e^{i\pi/2}$ , maka

w = iz = r \exp\left(i\left(\theta + \frac{\pi}{2}\right)\right)

dimana $z = re^{i\theta}$ , memutar setiap poin $z$ sebesar $\pi/2$ searah jarum jam. Sehingga

w = \bar{z} = x - iy

memetakan setiap poin $z$ ke refleksi simetrisnya terhadap sumbu real.

Mapping $w = z^2$

\begin{align*} w &= z^2 = (x + iy)^2\\ &= \underbrace{x^2 - y^2}_{u} + i\underbrace{2xy}_{v} \end{align*}

Jika kita memisalkan $u = c_1 = x^2 - y^2$ , maka $x = \sqrt{c_1 + y^2}$ sehingga terbentuk persamaan

u = c_1, \quad v = 2y\sqrt{y^2 + c_1} \quad (-\infty < y < \infty)

adalah fungsi parametrik hiperbola. Lalu jika kita memisalkan $v = c_2 = 2xy$ , maka $y = c_2/(2x)$ sehingga terbentuk persamaan

u = x^2 - \frac{c_2^2}{4x^2}, \quad v = c_2 \quad (0 < x < \infty)

yaitu sebuah fungsi parametrik hiperbola juga. Berikut adalah visualisasi dari Complex Variables and Applications.

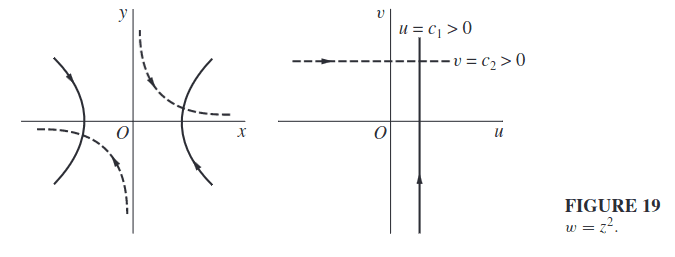
Tampak bahwa garis $c_1$ adalah parabola di bidang $xy$ yang diskontinu ketika melewati axis $u$ , sedangkan garis $c_2$ adalah parabola di bidang $xy$ yang diskontinu ketika melewati axis $v$ .

Mapping $w = e^z$

\begin{align*} w &= e^z = e^{x + iy}\\ &= e^x(\cos y + i\sin y) \end{align*}

Mapping ini memetakan setiap poin $z$ ke poin $w$ di bidang $uv$ sebagai koordinat polar. Garis vertikal di bidang $xy$ menjadi lingkaran di bidang $uv$ , serta garis horizontal di bidang $xy$ menjadi garis radial di bidang $uv$ .

Complex Limit

$f$ adalah kontinu dalam $z_0$ jika

\lim_{z \to z_0} f(z) = f(z_0)

Jika untuk setiap $\varepsilon > 0$ , terdapat $\delta > 0$ sehingga

|z - z_0| < \delta \quad \text{maka} \quad |f(z) - f(z_0)| < \varepsilon

Contoh:

f(z) = z/(z^2 + 1)

$f$ tidak kontinu di $\pm i$ karena $f(i) = 1/2i$ dan $f(-i) = -1/2i$ .
$f$ kontinu di $1$ karena $f(1) = 1/2$ dan $\displaystyle\lim_{z \to 1} f(z) = 1/2$ .

Theorems on Limits

Anggap $f(z) = u(x, y) + iv(x, y)$ dan

z_0 = x_0 + iy_0, \quad w_0 = u_0 + iv_0

maka $\displaystyle\lim_{z \to z_0} f(z) = w_0$ jika dan hanya jika

\lim_{(x, y) \to (x_0, y_0)} u(x, y) = u_0 \quad \text{dan} \quad \lim_{(x, y) \to (x_0, y_0)} v(x, y) = v_0

Jika $\displaystyle\lim_{z \to z_0} f(z) = w_0$ dan $\displaystyle\lim_{z \to z_0} g(z) = c_0$ , maka
- $\displaystyle\lim_{z \to z_0} [f(z) + g(z)] = w_0 + c_0$
- $\displaystyle\lim_{z \to z_0} [f(z)g(z)] = w_0c_0$
- $\displaystyle\lim_{z \to z_0} \left[\frac{f(z)}{g(z)}\right] = \frac{w_0}{c_0}, \quad c_0 \neq 0$
Untuk polinomial $P(z) = a_0 + a_1z + a_2z^2 + \ldots + a_nz^n$ , maka $\displaystyle\lim_{z \to z_0} P(z) = P(z_0)$ .
Jika $\displaystyle\lim_{z \to z_0} f(z) = w_0$ maka
- $\displaystyle\lim_{z \to z_0} f(z) = \infty \quad \text{jika} \quad \displaystyle\lim_{z \to z_0} \frac{1}{f(z)} = 0$
- $\displaystyle\lim_{z \to \infty} f(z) = w_0 \quad \text{jika} \quad \displaystyle\lim_{z \to 0} f(1/z) = w_0$
- $\displaystyle\lim_{z \to z_0} f(z) = \infty \quad \text{jika} \quad \displaystyle\lim_{z \to 0} \frac{1}{f(1/z)} = 0$

Exercises

Find the real and imaginary parts $u$ and $v$ of the given complex function $f$ as functions of $x$ and $y$ .

f(z) = \frac{\bar{z}}{z + 1}

Jawab:

Let's put $z = x + iy$ and $\bar{z} = x - iy$ and expand

\begin{align*} f(z) &= \frac{x - iy}{x + iy + 1} \times \frac{x - iy - 1}{x - iy - 1}\\ &= \frac{(x^2 + x - y^2) - i(2xy + y)}{(x + 1)^2 + y^2}\\ &= \underbrace{\frac{x^2 + x - y^2}{(x + 1)^2 + y^2}}_{u} - i\underbrace{\frac{2xy + y}{(x + 1)^2 + y^2}}_{v} \end{align*}

Compute the given complex limit using theorems on limits

\lim_{z \to 1 + i} \frac{z - \bar{z}}{z + \bar{z}}

Jawab:

f(z) = \frac{z - \bar{z}}{z + \bar{z}} = \frac{2yi}{2x}

\therefore f(z) = \frac{y}{x}i \quad \begin{cases}u = 0\\v = \frac{y}{x}i\end{cases}

from the given limit: $z_0 = 1 + i \Rightarrow x_0 = 1, y_0 = 1$

\begin{align*} u_0 &= \lim_{(x, y) \to (1, 1)} 0 = 0\\ v_0 &= \lim_{(x, y) \to (1, 1)} \frac{y}{x}i = i\\ \therefore & \lim_{z \to 1 + i} \frac{z - \bar{z}}{z + \bar{z}} = i \end{align*}

Roots of Complex Number Continuity and Differentiability

Function and Limit of a Complex Variable

Functions and Mappings

Complex Functions as Mappings

Mapping w=z2w = z^2w=z2

Mapping w=ezw = e^zw=ez

Complex Limit

Theorems on Limits

Exercises

Mapping $w = z^2$

Mapping $w = e^z$